Закономерности орбит планет и спутников

Если орбита следующей планеты в 2 раза дальше предыдущей (т.е., a₂ = 2 a₁), то период её орбиты будет примерно в 3 раза больше: 

T₂ = T₁ × √(2³/1) = T₁ × √8 ≈ 2,828 T₁ ≅ 3T₁.

§ 4.4. Орбитальные резонансы планет СС

Орбита следующей планеты с учетом поправки Ньютона: T₂ = √8 × T₁ (M + m₁) / (M + m₂). Т.е., если следующая планета меньше предыдущей, то ее резонанс лучше приблизится к 3:1, если больше - то сдвинется к 2,5 и может стать 5:2. Поэтому реально резонансы могут быть разные (табл. 2).

№	Планета	Расчётное расстояние, а.е.	Истинное расстояние, а.е.	Кратность осей	Период, зем.лет	Период, мерк.лет	Период в ΔTВен-Мерк	Другие резонансы
1	Меркурий	0,4	0,387	-	0,24	1	-	1/4 Зем, 2/5 Вен
2	Венера	0,7	0,723	1,5-2 Мер (1,85)	0,62	≅ 3 [?]	1 (0,38 з.л.)	~2/3 или 3/5 Зем
3	Земля	1,0	1,000	2,5 Мер	1,0	~4	1 (0,38 з.л.)	5/3 Вен
4	Марс	1,6	1,523	~2 Вен	1,88	~8	2,3 (0,88 з.л.)	3 Вен, ~2 Зем
5	Астероиды	2,8	2,20-3,65	2 Мар, 3 Зем, 3-5 (≅4) Вен, 7 Мер	4,6	19 (~20)	7,1 (2,7 з.л.)	7 Вен, ≅ 2 Мар
6	Юпитер	5,2	5,202	≅ 2 Аст, ≅ 7/2 или 10/3 Мар, 7 Вен	11, 9	50	19,2 (7,3 з.л.)	5/2 Аст, 6 Мар, 12 Зем, 19 Вен
7	Сатурн	10,0	9,538	2 Юп	29,5	123 (~120)	46,3 (17,6 з.л.)	5/2 Юп, 30 Зем, ≅ 40 Вен
8	Уран	19,6	19,182	2 Сат, ≅ 7 Аст	84,0	350	143,4 (54,5 з.л.)	≅ 3 Сат, 7 Юп
9	Нептун	38,8	30,058	3 Сат, 6 Юп, ≅ 10 Аст	164,8	687 (~700)	212,6 (80,8 з.л.)	2 Ур, 14 Юп
10	Плутон	77,2	39,44	2 Ур	248,5	1035 (~1050)	220,3 (83,7 з.л.)	3/2 Неп, 3 Ур, 8 Сат, 21 Юп

Табл. 2. Периоды обращения планет СА и их резонансы.

Наиболее простыми резонансами являются ¹/₂, ³/₂, ⁵/₂; ¹/₃, ²/₃; ³/₄; ²/₅, ³/₅; ³/₇, ⁴/7.

Положим их в последовательный ряд: 0,3 (1/3), 0,4 (2/5 и 3/7), 0,5 (1/2), 0,6 (3/5 и 4/7), 0,7 (2/3), 0,8 (3/4); 1,5 (3/2); 2,5 (5/2). Как видим, здесь находится место Меркурию, ВЫенере, Марсу, Фаэтону (астероидам).

Ряд этот получается слишком плотным - вероятно, из этих исключаются из-за гравитационного напряжения между объектами орбит. Полностью заполнится он может только для малых тел.

§ 4.5. Орбитальные правила для планет земной группы

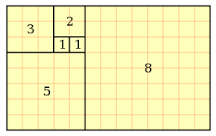
Гармонию и внутреннюю устойчивость характеризует ряд Фибоначчи [Владимирский 2013], который строится путём сложения соседних двух чисел, если ряд начать с двух единиц: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… Если в этом ряду делить число на предыдущее, то результат будет стремиться к 1,618. Это число называется Золотым сечением или числом Фидия (и числом Фибоначчи тоже называют). Число Фидия можно также вычислить по упрощенной формуле: Ф = (1 + √ 5) / 2 [Урманцев 2013, с. 19].

Рис. 1. Золотое сечение.

Расположим в ряд расстояния от Солнца до планет, выраженные в астрономических единицах:

0,39; 0,72; 1,0; 1,52; 2,8 (расчётное); 5,20; 9,54; 19,18; 30,06; 39,44 …

Умножим его на 5: 1,95; 3,6; 5; 7,6; 14; 26; 47,7; 95,9;150,3; 197,2.

Мы видим убедительное сходство, особенно для планет земной группы, относящихся к внутренней орбитальной зоне.

Получается, если орбиты планет-гигантов расположены друг к другу по удвоенным расстояниям (к Нептуну раньше это тоже могло относится), то орбиты земных планет раскладываются в ряд Фибоначчи. Правило же Тициуса-Боде вмещает в себя обе эти закономерности.

§ 4.6. Орбитальные пробелы в астероидах и кольцах Сатурна

Большую серию резонансных движений, воспринимаемых опять-таки как досадные помехи в стройной теории, доставляет пояс астероидов [Ипатов 2010, Молчанов 1974]. Хорошо известны щели (пробелы, люки) Кирквуда [Резонансы 2006, с.с. 9, 53], соответствующие резонансам 2:5, 1:3 с обращением Юпитера. Менее заметные понижения в кривой распределения периодов обращения астероидов возникают при резонансах 1:4, 1:5, 3:5, 3:7.

Существует и противоположная ситуация – группировка орбит вблизи точек 3:4 и 2:3.

В музыкальной терминологии это «кварта» и «квинта». «Прима» также устойчива и соответствует группе троянцев.

Знаменитая «щель Кассини» в Кольцах Сатурна имеет резонансную природу. Она занимает ту зону, в которой частички, составляющие кольца Сатурна, имели бы периоды, близкие к 1/2 периода Мимаса, 1/3 периода Энцелада и1/4 периода Тефии.

Для понимания этого явления недостаточно было обнаружить щель и открыть спутники Сатурна. С этим справился сам Кассини. Мало было даже открыть другие пробелы в кольцах Сатурна. Только в ХIХ веке Кирквуд, сопоставив пробелы в поясе астероидов с кольцами Сатурна, осознал единый резонансный Механизм образования пробелов.

§ 4.7. Орбитальные правила для транснептунов

Начиная с 30 а.е. (орбита Нептуна) начинается пояс Койпера [Витязев, с. 2; Кусков и др. 2009, с. 37], который продолжается примерно до 55 а.е. от Солнца. К этой области принадлежит карликовая планета Плутон.

На самой орбите Плутона находятся резонансные ему плутино, чьи 3 оборота равны 4 оборотам Нептуна ~220 лет.

Далее открытые малые планеты располагаются «слоями» (возможно, не все еще открыты, возможно, имеют место щели и пробелы, как в астероидах и кольцах Сатурна, под влиянием неких более массивных космических тел).

От 40 до 60 а.е. (период обращения 250-290 лет) малые планеты идут сплошным массивом.

Следующий слой уже закойперовских планет начинается с 80 а.е., потом – примерно со 100 а.е. (орбитальный период от 500 лет).

Заслуживает внимание резонанс 3-х малых планет, имеющих резонанс 1:2:4:

1. Плутоид Варуна, или 2000 WR106 - 43 а.е., 282 г.
2. Трансплутон Эрида (также Ксена, Зена, или 2003 UB313 - 97 а.е., 560 лет.
3. Объект 2014 UZ224 - примерно 155 а.е., 1136 лет.

В этой связи уместно опять вспомнить правило Тициуса-Боде и продолжить наш список «законных» орбит СС: 40, 80, 160, 320, 640, 1280... Дальше продолжать не имеет смысла, ибо любая планета, расположенная далее 600 а.е., должна сойти со своей орбиты. И мы видим, что упомянутые 3 резонансные планеты как раз лежат на расчетных орбитах 40, 80 и 160. А самой дальней извесной планетой за поясом Койпера является Седна, находящаяся в 500 а.е. от Солнца, не считая некой «планеты X», открытой на кончике пера, и находящейся, действительно, на самом краю СС – в 600 а.е. или даже дальше, которая уже вписывается в классическую расчетную орбиту 640 а.е.

§ 4.8. Особенности орбит спутников планет-гигантов

Системы спутников планет-гигантов [Астрономия 2009, с. 568] имеют общую структуру - они состоят из 3 зон:

1. внутренней, где расположены спутники существенно меньшего размера (часто - астероиды), чем в центральной зоне;
2. центральной, где представлены «классические» спутники с устоявшимися круговыми орбитами;
3. внешней, где находятся, в основном, астероиды, случайно захваченные планетой (яркий пример - Феба - самая дальняя из известных сатурнианских лун) [Симоненко 1985, с. 79].

Нас сначала будут интересовать закономерности орбит спутников центральной зоны. И здесь можно увидеть 2 подтипа:

1. примерно одинаковые по размерам и плотности спутники, как галилеевские спутники Юпитера или классические спутники Сатурна
2. и спутники меньшего размера, но с одним самым крупным, как Титан на Сатурне или Титания на Уране, Тритон на Нептуне.

Последний случай напоминает планеты Солнечной системы,так же состоящие из 3 зон и очень крупным Юпитером в центральной зоне. Посмотрим, как будут соответствовать закономерности орбит спутников в этих 2-х подтипах.

Особенности орбит спутников Юпитера

Орбитальные характеристики спутников Юпитера (центральные, или «галилеевские», выделены розовым) - см. табл. 3:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Юпитера
Метида	128	0,3	(40)
Адрастея	129	0,3	(25)
Амальтея	181	0,5 ~ 3/2 = 5/3 TАдр	195*
Теба	221	0,7 ~ 3/2 TАма	(80)
II. Центральные ("галилеевские") спутники Юпитера
Ио	422	1,8 = 5/2 TТеб	3640
Европа	671	3,6 = 2 TИо	3130
Ганимед	1070 = 1,5 RЕв	7,2 = 2 TЕвр	5280
Каллисто	1883	16,7 ~ 5/2 TГан	4850
III. Ближние внешние спутники Юпитера
Леда	11094	239 ~ 14 TКал	(15)
Гималия	11480	251	170
Лиситея	11720	259	(20)
Элара	11737	260	80
IIV. Дальние внешние спутники Юпитера
Ананке	21200	631	(20)
Карме	22600	692	(30)
Пасифе	23500	735	(40)
Синопе	23700	758	(30)

Табл. 3. Периоды обращения юпитерианских спутников.

Видим, что первые 3 галилеевских спутника имеют радиусы орбит примерно в 1,5 (точнее - в 1,59) раз больше предыдущего и периоды в 2 раза больше, чем у предыдущего спутника.
Это можно выразить формулой [Мюррей 2010, с. 30; Сурдин 2009, с. 62]: 1/T_Ио - 3/T_Евр + 2/T_Ган = 0.

Особенности орбит спутников Сатурна

Орбитальные характеристики спутников Сатурна (центральные, или «классические», выделены розовым) - см. табл. 4:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Сатурна
Пан	134	0,6	(20)
Атлант	138	0,6	(30)
Прометей	139	0,6	(110)
Пандора	142	0,6	(100)
Эпиметей	151	0,7	(130)
Янус	151	0,7	190
II. Центральные спутники Сатурна
Мимас	186	0,9	390
Энцелад	238	1,4	500
Тефия	295	1,9	1060
Телесто	295	1,9	(30)
Калипсо	295	1,9	(30)
Диона	377	2,7	1120
Елена	377	2,7	(35)
Рея	527	4,5	1530
Титан	1222	15,9	5150
Гиперион	1481	21,3	300
Япет	3561	79,3	1460
III. Внешние спутники Сатурна
Феба	12952	550,5	(220)

Табл. 4. Периоды обращения сатурнианских спутников.

Особенности орбит спутников Урана

Орбитальные характеристики спутников Урана - см. табл. 5:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Урана
Корделия	50	0,3	(25)
Офелия	54	0,4	(30)
Бианка	59	0,4	(40)
Крессида	62	0,5	(60)
Дездемона	63	0,5	(50)
Джульетта	64	0,5	(80)
Порция	66	0,5	(110)
Розалинда	70	0,5	(50)
Белинда	75	0,6	(70)
Пэк	86	0,8	(150)
II. Центральные спутники Урана
Миранда	129	1,4	480
Ариэль	191	2,5	1160
Умбриэль	266	4,1	1170
Титания	436	8,7	1580
Оберон	584	13,5	1520
III. Внешние спутники Урана
Калибан	7169	580	(60)
Сикоракса	12214	1290	(120)

Табл. 5. Периоды обращения уранианских спутников.

Особенности орбит спутников Нептуна

Орбитальные характеристики спутников Нептуна - см. табл. 6:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Нептуна
Наяда	48	0,3	(50)
Таласса	50	0,3	(80)
Деспина	53	0,3	(150)
Галатея	62	0,4	(160)
Ларисса	74	0,6	(200)
II. Центральные спутники Нептуна
Протей	118	1,1	420
Тритон	355	5,9	2700
III. Внешние спутники Нептуна
Нереида	5513	360,2	340

Табл. 6. Периоды обращения нептуновых спутников.

Что забавно, периоды Галатеи, Лариссы, Протея и Тритона соотносятся как расстояния в а.е. от Солнца до Меркурия, Венеры, Земли и Юпитера (см. табл. 1, 2).

§ 4.9. Орбитальные правила расположения экзопланет

Примерно треть открытых экзопланет входит в мультипланетные системы, которых известно уже более 130. Наличие орбитальных резонансов там широко распространено. Известные системы с резонансом 2:1 - Gliese 876 и HD 82943, с резонансом 3:1 - 55 Cnc. У Gliese 876 резонансы как у галилеевских спутников Юпитера: 4:2:1 ("резонанс Лапласа"). А недавно открыта плотно упакованная планетами резонансная система Kepler 223, у которой такой резонансный ряд еще длиннее: 8:4:2:1 [Маров 2017, с. 63].

В Галактике у большинства звезд с экзопланетами самые массивные из них расположены не на наибольшем удалении от светил, а рядом с ними (ближе, чем Меркурий к Солнцу) - там находятся горячие экзопланеты с небольшими периодами вращения.

В феврале 2017 года была открыта экзопланетная система TRAPPIST-1. Вокруг красного карлика обращается 7 планет, 6 из которых находятся в цепочке резонансов 2:3:4:6:9:15:24. Видно, что здесь средний множитель для следующей орбиты - 1,5, - как в земной группе. Возможно, это особенность всех близких орбит. Далее, по аналогии, в этой звёздной системе могут быть планеты с резонансами 36:54.

5. Природа явления

Перейдём от астрономических исследований (того, что видим) к физическим (того, что не видим). Попытаемся установить: 1) законы формирования резонансной конфигурации в мультиорбитальной системе; 2) физический смысл правила Тициуса-Боде (если он есть), уточнив его и выразив через переменные.

§ 5.1. Кратности и разности в резонансах

§ 5.2. Суммарные гравитационные потенциалы на орбитах

§ 5.3. Физический смысл закона Тициуса-Боде и его уточнение

6. Применение полученных знаний

§ 6.1. Вычисение "на кончике пера" новых орбит

На основании правил распределения транснептуновых планет (см. § 4.7) и уточненного закона Тициуса-Боде (см. § 5.3) для них можно предположить наиболее вероятные орбиты пока не найденных новых планет Солнечной системы.

§ 6.2. Восстановление предыдущих конфигураций орбит

На основании правила Тициуса-Боде пока весьма осторожно можно высказаться о том, что Нептун был на средней орбите Плутона (40 а.е.). Видимо, именно Нептун сформировал пояс Койпера. Сам Плутон, возможно, был спутником Нептуна.

Сами спутники Нептуна, вероятно, принадлежали поясу Койпера. Это можно эскизно исследовать по их плотностям.

Причиной орбитальной перестройки мог быть массивное космическое тело (транзитная экзопланета или планета-гигант пролетающей мимо звезды из ближайшего окружения Солнца), проходившая перпендикулярно плоскости эклиптики. Например, звезда Шольца, которая сейчас отстоит на 20 световых лет, 50 тысяч лет назад приблизилась к Солнечной системе и даже пересекла Облако Оорта (кометный резервуар). В это время ее расстояние до центра Солнца было 0,8 световых лет (52 000 а.е. или 8 трлн км) — это в 5 раз ближе, чем нынешняя ближайшая звезда Проксима Центавра. В более далёкие времена это могли быть другие звёзды.

Это космическое событие могло быть причиной и поворота Урана по оси на 90°.

§ 6.3. Предсказание перестройки орбитальных систем

§ 6.4. Влияние конфигураций планет на Солнце и Землю

7. Заключение

В данном исследовании получены следующие результаты:

1. Орбиты планет СС делятся на 3 зоны (земные, гиганты, койперовские), для расстояний в которых разные правила.
2. Орбиты планет земного типа (до Юпитера) выстраиваются в ряд Фибоначчи.
3. Планеты-гиганты имеют 2-кратную дальность относительно предыдущей. При этом их резонансные характеристики близки к 3:1.
4. Транснептуновые планеты «лежат слоями» через 20 а.е.
5. Правило Тициуса-Боде (ПТБ) хорошо описывает орбиты первых 2-х групп. В целом, оно является правилом удвоения, только для первых планет применяется множитель не 2, а число Фидия (1,618), характеризующее Золотое сечение.
6. Исключение составляют Нептун и Плутон, но эти исключения лишь подтверждают правило, т.к. Нептун был на орбите нынешнего Плутона , который был его спутником.
7. Орбиты спутников планет-гигантов также делятся на 3 зоны: внутренние астероиды, срединные классические, внешние астероиды.
8. Орбиты в первой и последней группах могут иметь незакономерный характер (и сами эти астероиды имеют сильный эксцентриситет и могут иметь большой наклон к орбите других спутников).
9. У классических спутников можно найти свои правила расположения.

8. Глоссарий

Некоторые термины и аббревиатуры, встречающиеся в статье:

• ПГ - планеты-гиганты (Юпитер, Сатурн, Уран, Нептун).
• ПЗГ - планеты земной группы (Меркурий, Венера, Земля, Марс).
• СА - солнечная активность, определяемая количеством солнечных пятен (индексируемых числом Вольфа).

9. Литература

• Астрономия: век XXI. / Ред.-сост. Сурдин В.Г. – Фрязино: "Век 2", 2008. – 2-е изд., испр. и доп. – 608 с.: ил. [Есть в Озоне.]
• Витязев А.В., Печерникова Г.В. Происхождение малых тел Солнечной системы. - 5 с. Статья подарена автором в виде распечатки.
• Владимирский Б.М. Солнечная активность и общественная жизнь. Космическая историометрия: от первых российских космистов до наших дней. - М.: Кн.дом "ЛИБРОКОМ", 2013. – 192 с. [Есть в URSS.]
• Гаршин И.К. Космический ритм экологических кризисов и дальних миграций кочевников Евразии. // Материалы выездной сессию 11-й Крымской конференции «Космос и биосферы» в Санкт-Петербурге в рамках 7-го конгресса «Слабые и сверхслабые поля и излучения в биологии и медицине» (7–11 сентября 2015); Симпозиум B. «Слабые воздействия на организменном и популяционном уровне и устойчивость жизненных процессов в биосфере. Экологические и социальные последствия слабых воздействий», С. 133.
• Ипатов С.И. Миграция небесных тел в Солнечной системе. - М.: Физматлит, 2010. – 320 с. [Есть в Озоне.]
• Кусков О.Л., Дорофеева В.А., Кронрод В.А., Макалкин А.Б. Системы Юпитера и Сатурна: Формирование, состав и внутреннее строение крупных спутников / Отв. ред. М.Я. Маров. - М.: Изд. ЛКИ, 2009. - 576 с.
• Маров М.Я., Шевченко И.И. Экзопланеты. Экзопланетология. - М.-Ижевск: Институт компьютерных исследований, 2017. - 138 с.
• Молчанов А.М. Гипотеза резонансной структуры Солнечной системы. - Препринт. Пущино: НЦБИАН СССР, 1974. - 19 с.
• Мюррей К., Дермотт С. Динамика Солнечной системы. / Пер. с англ. под ред. И.И. Шевченко. - М.: Физматлит, 2010. - 588 с.
• Резонансы в небесной механике / Сб. работ. - Москва-Ижевск: Ин-т компьютерных исследований, 2006. - 316 с.
• Симоненко А.Н. Гипотеза резонансной структуры Солнечной системы. - М.: Наука, Гл. ред. физ.-мат. лит-ры. - 1985. - 208 с.
• Солнечная система. / Ред.-сост. Сурдин В.Г. - М.: ФИЗМАТЛИТ, 2009. - 400 с. - (Астрономия и астрофизика).
• Урманцев Ю.А. Симметрия природы и природа симметрии. Философские и естественно-научные аспекты. Изд. 4-е. - М.: Книжный дом "ЛИБРОКОМ", 2013. - 232 с.

10. Благодарности

Сердечное спасибо оргкомитету международной крымской конференции "Космос и биосфера" за разрешение выступить с докладом, ставшим анонсом этой статьи. И особо я признателен председателю оргкомитета Владимирскому Борису Михайловичу за библиографическую помощь и научные советы.

11. Дополнительные сведения о статье

Доклад по данной теме впервые был зачитан в октябре 2017 года на XII Международном конгрессе "Космос и биосфера" в Алуште (Крым).

Забавен результат создания резюме этой статьи нейронной сетью Яндекса (под заголовком "Закономерности планетарных орбит (Игорь Гаршин)"):

1. Статья посвящена орбитальным закономерностям в Солнечной системе.
2. Орбиты планет делятся на 3 зоны: земные, гиганты и койперовские.
3. Орбиты планет земной группы выстраиваются в ряд Фибоначчи.
4. Планеты-гиганты имеют 2-кратную дальность относительно предыдущей.
5. Правило Тициуса-Боде хорошо описывает орбиты первых 2-х групп.
6. Орбиты спутников планет-гигантов также делятся на 3 зоны.
7. Физический смысл правила Тициуса-Боде и его уточнение уточнены.
8. Применение полученных знаний включает вычисление "на кончике пера" новых орбит и восстановление предыдущих конфигураций орбит.

---